Час 5 - Корњача графика - гранање, угнежђене петље, процедуре, торке/листе¶
Гранање¶
Приликом цртања неких фигура корњача наизменично треба да извршава
одређене врсте наредби. На пример, приликом цртања испрекидане линије
корњача у сваком кораку помера напред и након сваког померања или
подиже или спушта оловку и то чини наизменично (напред, подигни,
напред, спусти, напред, подигни, напред, спусти). То је могуће постићи
тако што се у сваком кораку петље испитује да ли је вредност бројача
парна или непарна тј. да ли при дељењу са два даје остатак 0 (као што
ћемо детаљније описати у поглављу о израчунавању, у језику Python се остатак при
дељењу броја i са 2 може израчунати помоћу i % 2). Гранање,
тј. условно извршавање наредби, постижемо помоћу наредбе if-else.
Испрекидана линија¶
Нацртај поново испрекидану линију, али овај пут коришћењем гранања.
Корњача иде напред 10 пута, при чему пет пута од тога има подигнуту, а пет пута има спуштену оловку. Дакле, уведи петљу чије се тело понавља пет пута, у телу петље помери корњачу за 20 корака, а затим или подигни или спусти оловку, тако да то буде наизменично (то можеш реализовати тако што ћеш у парним корацима подизати, а у непарним корацима спуштати оловку). Имајући ово у виду исправи наредни програм тако да црта испрекидану линију.
Звезда без пресецања¶
Напиши програм у којем корњача црта звезду без цртања унутрашњег петогула, као на следећој слици.

Звезду можемо нацртати тако што нацртамо десет дужи (десет кракова једнакокраких троуглова који представљају краке звезде). Након цртања сваке од тих дужи окрећемо се и то наизменично налево за \(72^\circ\) (када смо у дну крака) па надесно за \(144^\circ\) (када смо на врху крака). Поново наизменично изршавање наредби (овај пут окретања) можемо остварити тако што проверавамо парност бројачке променљиве.
Угнежђене петље¶
У сложенијим задацима имамо потребу да се облици који се ицртавају коришћењем петљи понављају неколико пута. Тако се добијају програми који садрже петље у чијем телу се налазе друге петље. Такве петље називају се угнежђене петље. Урадимо неколико примера овог облика.
Три квадрата¶
Напиши програм којим корњача црта мало сложенији облик који се састоји од три квадрата, окренутих за по 120 степени један у односу на други, као на слици.
По сличном принципу можемо нацртати и наизглед доста сложеније облике.
Компликованија звезда¶
Напиши програм у којем корњача црта звездицу приказану на слици. Она се састоји од 20 троуглова чија је страница дугачка 60 корака, који су распоређени око правилног двадесетоугла чија је дужина странице 10 корака.
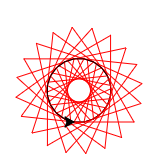
Исправи наредни програм тако да се добије облик са слике.
Напиши програм који исцртава десет квадрата који имају заједничко доње лево теме и чије су дужине страница редом 10, 20, 30, 40 и тако даље.
Процедуре¶
Угнежђене петље се могу избећи, а програми се могу учинити много разумљивијим ако се уведу процедуре за цртање основних облика.
Процедура за цртање многоугла¶
Приметимо да се цртање многоугла (каже се и полигона) јавило у више различитих програма. Стога је корисно дефинисати процедуру за цртање многоугла. Параметри те процедуре биће број страница полигона и дужина једне странице.
Дефиниција процедуре започета је кључном речју def након чега је
наведен назив процедуре (у нашем примеру, то је био poligon), а
након тога параметри процедуре у заградама. Након двотачке, наведен је
програмски код који чини тело процедуре, увучен у односу на прву
линију (слично као што је и тело наредби for, while и if
увек увучено). Тело сачињавају наредбе које се извршавају сваки пут
када се процедура позове.
Дефинисањем процедуре дефинисали смо заправо нову наредбу коју можемо
користити у пруграму. Након ове дефиниције, квадрат димензије 100
пиксела нацртаћемо тако што наведемо poligon(4, 100), а шестоугао
димензије 50 тако што наведемо poligon(6, 50). Са процедуром за
цртање многоугла на располагању, наш програм за цртање три квадрата
различите боје је доста једноставније написати и постаје доста
разумљивији.
Покушај да измениш претходни програм тако да уместо квадрата црта три шестоугла дужине страница 80 корака.
Четири квадрата¶
Напиши програм у којем корњача црта облик који се састоји од четири квадрата, како је приказано на наредној слици.
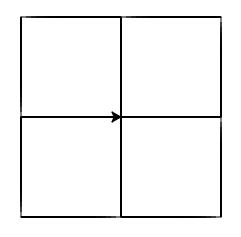
Дефиниши процедуру за цртање квадрата, а затим размисли како су ти квадрати међусобно распоређени, тј. колико треба да се окрене корњача након завршетка цртања сваког квадрата.
Решење са петљом у петљи.
Решење са помоћном процедуром за цртање квадрата.
Торке/листе¶
Некада желимо да се у сваком кораку петље користи различита вредност. Најједноставнији начин да тако нешто постигнемо је да употребимо торку тј. листу вредности (о чему ће бити много више речи у поглављу о структурама података). Погледајмо пар примера ове технике.
Шарени квадрат - петља¶
Допуни претходни програм тако да црта шарени квадрат, чије су боје страница редом црвена, зелена, плава и жута.
За решавање задатка нам је згодно да употребимо торку у којој ћемо
упамтити четири ниске које представљају називе те четири боје на
енглеском језику (такву торку можемо дефинисати помоћу boje =
("red", "green", "blue", "yellow")). У сваком кораку петље, боју
ћемо постављати на i-ти елемент те торке, где је i бројачка променљива
која редом узима вредности 0, 1, 2 и 3 (i-том елементу торке boje
можемо приступити навођењем boje[i]). У наредном програму опет има
неколико грешака и твој задатак је да их исправиш.
Звезда без пресецања¶
Напиши програм у којем корњача црта звезду без цртања унутрашњег петогула, као на следећој слици.

Овај задатак смо већ решавали уз помоћ гранања, али решење можемо
добити и уз помоћ двочлане листе. У листу можемо поставити углове од
72 и -144 степена и у сваком кораку се окретати улево за један од та
два угла (окрет удесно за 144 степена је једнак окрету улево за -144
степена), наизменично. Угловима из листе приступамо наизменично,
тј. приступамо угловима на позицији 0, затим 1, па 0, па 1, и тако
даље. Ово можемо остварити тако што у сваком кораку приступимо углу у
листи на позицији која се добије као остатак при дељењу променљиве
i бројем два (подсетимо се, тај остатак можемо израчунати помоћу
i % 2). У складу са тим исправи наредни програм.
Домаћи задатак¶
Шарени облик¶
Наредни интересантан облик се добија тако што корњача црта црвену линију дужине 50 и затим се налево окреће за 31 степен, затим црта зелену линију дужине 70 и окреће се налево за 71 степен, затим црта плаву линију дужине 90 и окреће се налево за 101 степен након чега се цртеж наставља по истом принципу. Напиши програм који анализом остатка при дељењу са 3 бројача у петљи одређује шта треба да уради.
Квадрат шарених ивица¶
Дефиниши процедуру за цртање линије у којој се насумично смењују дужи две боје. Параметри процедуре треба да буду број дужи, дужина сваке дужи и две боје. Употреби процедуру да нацрташ квадрат коме ће ивице бити састављене од таквих линија.

